Deadlock, Circular Reference and Halting
Deadlock
Deadlock can be understood via resource allocation graph.
It has two kinds of nodes:
- The unit of execution: Threads, processes, goroutines, async tasks, etc.
- Synchronization primitives: Locks, channels, etc.
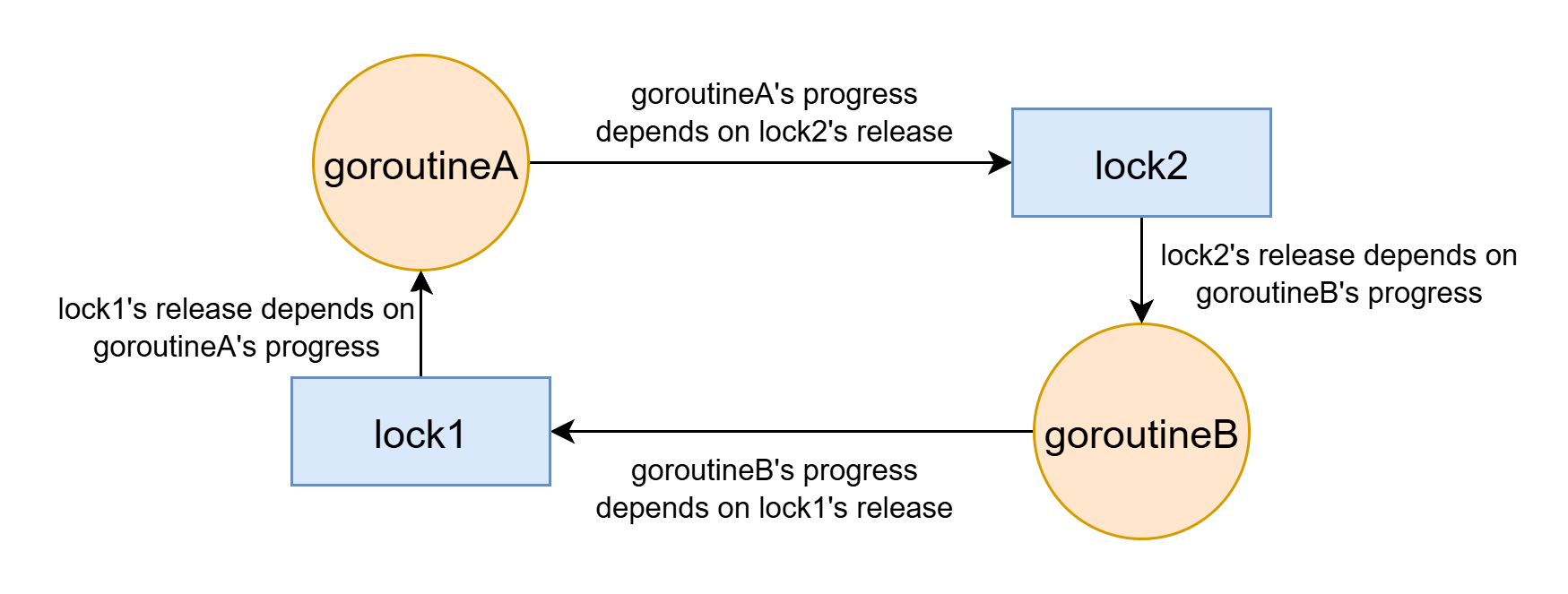
Its edges represent dependency. A point to B means A depends on B. Specifically it has two kinds of edges:
- Assignment edge. A lock points to a thread. It denotes that the thread already holds the lock. The lock's release depends on the thread's progress.
- Request edge. A thread points to a lock. It denotes that the thread try to hold the lock. The thread's progress depends on acquiring the lock.
Deadlock occurs when that graph forms a cycle.
A simple two-lock deadlock in Golang:
func goroutineA(lock1 *sync.Mutex, lock2 *sync.Mutex) {
lock1.Lock()
defer lock1.Unlock()
// ...
lock2.Lock() // deadlock here
defer lock2.Unlock()
}
func goroutineB(lock2 *sync.Mutex, lock1 *sync.Mutex) {
lock2.Lock()
defer lock2.Unlock()
// ...
lock1.Lock() // deadlock here
defer lock1.Unlock()
}
Resource allocation graph in deadlock state:
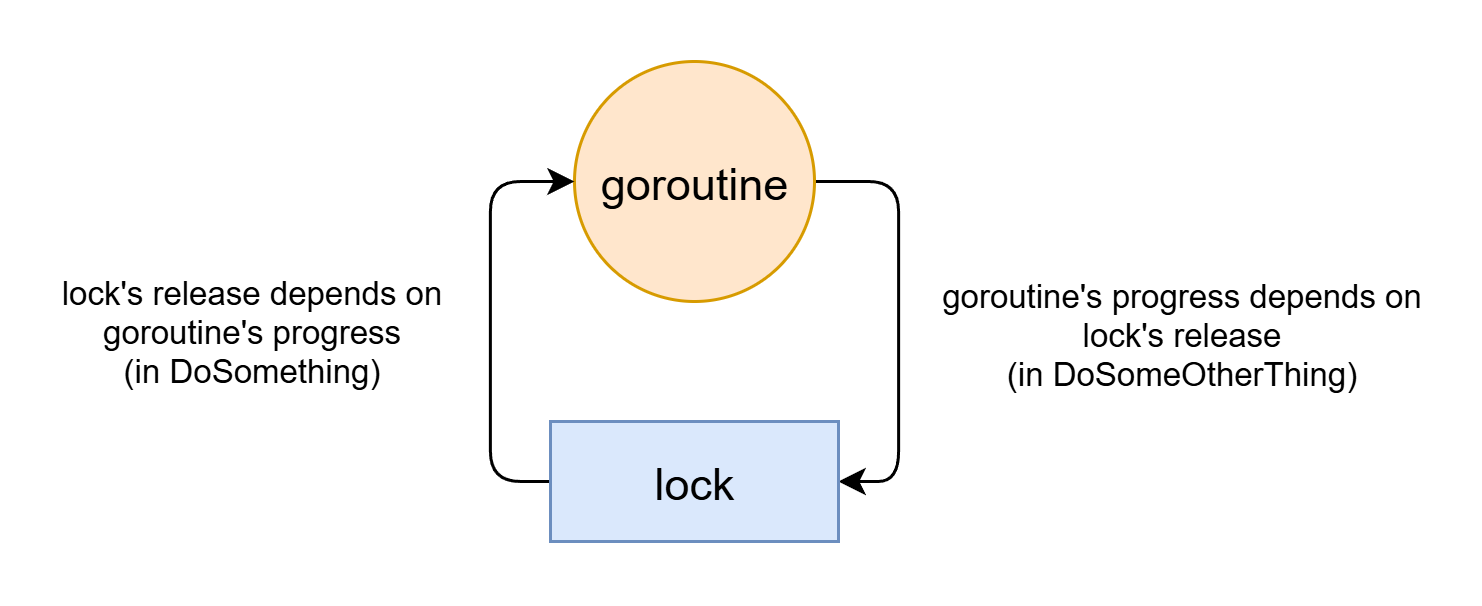
Golang's locks are not re-entrant. Deadlock can happen with only one lock and one thread:
type SomeObject struct {
lock *sync.Mutex
// ...
}
func (o *SomeObject) DoSomething() {
o.lock.Lock()
defer o.lock.Unlock()
// ...
o.DoSomeOtherThing()
}
func (o *SomeObject) DoSomeOtherThing() {
o.lock.Lock() // deadlock here
defer o.lock.Unlock()
// ...
}
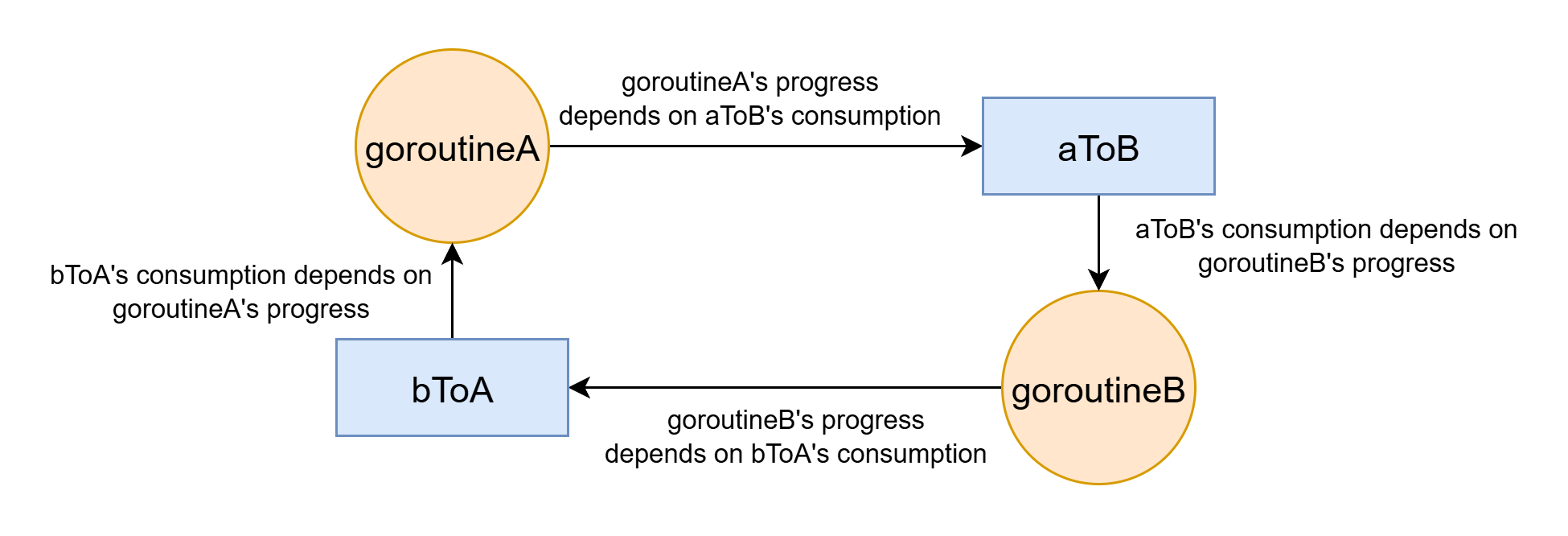
Lock-free deadlock
Deadlock can also happen when there is no explicit lock. I call it lock-free deadlock. (The naming is similar to "serverless servers", "constant variables" and "unnamed namespaces".)
A simple Golang program showing lock-free deadlock:
func goroutineA(aToB chan string, bToA chan string) {
aToB <- "Hello from A" // deadlock here
msg := <-bToA
}
func goroutineB(aToB chan string, bToA chan string) {
bToA <- "Hello from B" // deadlock here
msg := <-aToB
}
In Golang, channels are not buffered by default, then producer waits for consumer. If the two channels are not buffers, it will deadlock:
If you put a thing into a channel that no one will consume, it will wait forever. But changing the channel to buffered channel make(chan string, 1) will make the producer to not wait for consumer as long as buffer is not full. That deadlock can be solved by making channels buffered.
Note that Golang channel buffer must have a constant size limit. There are packages for unbounded channel (chanx). However the memory may be not large enough if big bursts occurs. Use disk-backed event queue (e.g. Kafka) to get larger buffer capacity.
Note that sometimes you need back pressure (stop producer when buffer is full) to improve stability (e.g. avoid using up memory) at the cost of blocking (and rejecting) requests.
Buffered channels can still deadlock
The previous deadlock can be solved by making channel buffered. However, buffering doesn't solve all lock-free deadlocks. For example:
func goroutineA(aToB chan string, bToA chan string) {
msg := <-bToA // deadlock here
aToB <- "Hello from A"
}
func goroutineB(aToB chan string, bToA chan string) {
msg := <-aToB // deadlock here
bToA <- "Hello from B"
}
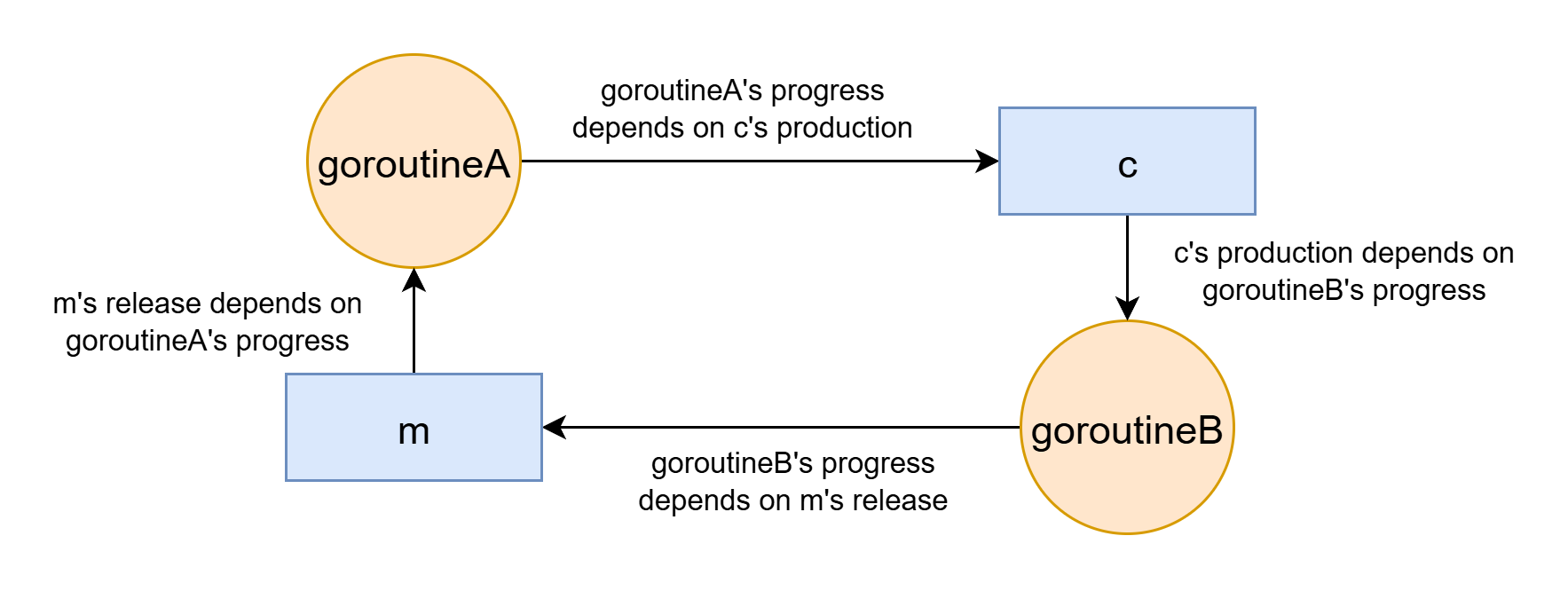
Channel+Lock deadlock
Example:
func goroutineA(m *sync.Mutex, c chan string) {
m.Lock()
defer m.Unlock()
value := <-c // deadlock here (assume goroutineA runs first)
}
func goroutineB(m *sync.Mutex, c chan string) {
m.Lock() // deadlock here (assume goroutineA runs first)
defer m.Unlock()
c <- "some result"
}
Select leak
For example, do some work with timeout, using channel and select:
func doWorkWithTimeout(timeout time.Duration) (string, error) {
ch := make(chan string) // unbuffered channel
go func() {
result := doWork()
ch <- result // this blocks
}()
select {
case result := <- ch:
return result, nil
case <- time.After(timeout):
return "", errors.New("timeout") // if this path is taken, ch will never be consumed
}
}
select will finish if either case gives a result. If it timeouts, select will finish by second case and never consume from ch. So the ch <- result will hang forever, causing goroutine leak. This can be fixed by making ch buffered.
Many memory leaks in Golang are caused by goroutine leak. Goroutine leak will also cause its task to never finish which can cause other bugs. If something waits for a leaked goroutine it will deadlock.
Select also has traps in async Rust, but in a different mechanism (cancellation).
Livelock
Sometimes, replace locking with try-locking and add retrying mechanism can solve some deadlock. But it may also introduce livelock: keep retrying without successfully acquiring lock.
func WithRetry[T any](attempts int, operation func() (T, error)) (T, error) {
i := 0
for {
result, err := operation()
if err == nil {
return result, nil
}
i++
if i >= attempts {
return result, err
}
}
}
func goroutineA(lock1 *sync.Mutex, lock2 *sync.Mutex) (string, error) {
return WithRetry(10, func() (string, error) {
lock1.Lock()
defer lock1.Unlock()
// do some work
if lock2.TryLock() { // this may keep failing
defer lock2.Unlock()
// do some other work
return "success", nil
} else {
return "", fmt.Errorf("failed to acquire lock2")
}
})
}
func goroutineB(lock1 *sync.Mutex, lock2 *sync.Mutex) (string, error) {
return WithRetry(10, func() (string, error) {
lock2.Lock()
defer lock2.Unlock()
// do some work
if lock1.TryLock() { // this may keep failing
defer lock1.Unlock()
// do some other work
return "success", nil
} else {
return "", fmt.Errorf("failed to acquire lock1")
}
})
}
Priority inversion
In some real-time (or near-real-time) systems, important threads have higher priority than other thread. The thread scheduler tries to run higher-priority threads first.
Priority inversion problem can make high-priority threads keep stuck, effectively similar to deadlock (although it's not strictly deadlock).
The common priority inversion problem involves 3 threads, with low/medium/high priorities respectively:
- The low-priority thread holds a lock.
- A high-priority thread tries to acquire lock. It cannot and wait for low-priority thread to release lock.
- Another medium-priority thread keeps running. When medium-priority thread runs, it occupies CPU cores so that low-priority thread cannot run. The high-priority thread's running now indirectly depend on medium-priority thread. If medium-priority thread keeps running, high-priority thread will never run.
Circular reference counting leak
Reference counting leaks memory if there exists a cycle of strong references.
- Reference counting works locally. It only tracks how many references point to one object. It only triggers when references to one object adds/removes.
- Tracing GC works globally. It knows all GC roots and scans the whole object graph.
- Cycle is a global property. If the cycle can be arbitrarily large, no local-only mechanism can detect a cycle. However if you limit the cycle size (e.g. at most 3-node cycle) then it's a local property and can be detected by local mechanisms.
The common solution is to use weak reference counting to cut cycle, as developers know the reference structure and know where cycles can form.
Observer circular dependency
Observer pattern is common in GUI applications. It's a common pattern to use observer to make some data's update to propagate to other data. However, it may form a circular dependency, then stuck in dead recursion:
type ObservedValue[T any] struct {
Value T
Observers []func(T)
}
func (o *ObservedValue[T]) AddObserver(observer func(T)) {
o.Observers = append(o.Observers, observer)
}
func (o *ObservedValue[T]) SetValue(value T) {
o.Value = value
for _, observer := range o.Observers {
observer(value)
}
}
func main() {
a := ObservedValue[int]{Value: 0}
b := ObservedValue[int]{Value: 0}
a.AddObserver(func(value int) {
b.SetValue(value + 1)
})
b.AddObserver(func(value int) {
a.SetValue(value + 1)
})
a.SetValue(1) // stuck in dead recursion
}
Similar thing can happen in React:
function SomeComponent() {
const [countA, setCountA] = useState(0);
const [countB, setCountB] = useState(0);
useEffect(() => {
setCountB(countA + 1);
}, [countA]);
useEffect(() => {
setCountA(countB + 1);
}, [countB]);
...
}
React effect triggers in next iteration of event loop so it won't directly dead recursion, but it will keep doing re-render which costs performance.
Ordering breaks cycle
If there is a globally uniform ordering of acquiring locks, then deadlock won't occur.
For example, if there are two locks lock1 and lock2, if I ensure that lock1's locking order if before lock2, then there won't be the case that a thread acquired lock2 and is acquiring lock1. Then in resource allocation graph, the path from lock2 to lock1 cannot be formed. So deadlock can be prevented.
Rust favors tree-shaped ownership. There is a hierarchy between owner and owned values. This creates an order that prevents cycle. If you use sharing (reference counting) but don't use mutability, then creating new value can only use already-created value, so circular reference is still not possible. Only by combination of sharing and mutability can circular reference be created.
Without mutability and lazy evaluation, reference cycle cannot be created. Because new values can only contain the existing values when creating it (order of evaluation prevents cycle). But with lazy evaluation, the not-yet-created values can be used so circular reference is possible.
Lazy evaluation circular reference
Infinite container
Haskell is a pure functional language where there is no mutable state. Haskell also has lazy evaluation.
Haskell has lazy evaluation so it allows circular reference. Example:
ones :: [Integer]
ones = 1 : ones
It will be an infinte list of 1s.
It can also be seen as a tree structure expand infinitely, with no circular reference.
Similarily, this
from :: Integer -> [Integer]
from n = n : from (n + 1)
creates an infinite list of increasing integers from n.
Although the conceptual list is infinitely large, due to lazy evaluation, only the needed places need to be computed and stored into memory. They can be used as long as computation don't use the whole list.
Reverse state monad
In normal state monad, the new state is computed on old state. But in reverse state monad, the state flows backwards. Old state can be computed on new state. You can change the old state that's used in previous computation. This "magic" relies on lazy evaluation.
Definition of reverse state monad.
newtype RState s a = RState { runRState :: s -> (a, s) }
instance Monad (RState s) where
...
RState sf >>= f = RState $ \state2 ->
let (oldResult, state0) = sf state1
(newResult, state1) = runRState (f oldResult) state2
in (newResult, state0)
It has circular dependency: (oldResult, state0) = sf state1 uses state1 obtained in next line. The next line uses oldResult obtained in previous line.
Example usage:
{-# LANGUAGE GeneralizedNewtypeDeriving #-}
import Control.Monad (ap)
newtype RState s a = RState { runRState :: s -> (a, s) }
instance Functor (RState s) where
fmap f st = RState $ \s ->
let (a, s') = runRState st s
in (f a, s')
instance Applicative (RState s) where
pure x = RState $ \s -> (x, s)
(<*>) = ap
instance Monad (RState s) where
return = pure
RState sf >>= f = RState $ \state2 ->
let (oldResult, state0) = sf state1
(newResult, state1) = runRState (f oldResult) state2
in (newResult, state0)
get :: RState s s
get = RState $ \s -> (s, s)
put :: s -> RState s ()
put s = RState $ \_ -> ((), s)
-- it modifies old state based on new state
modify :: (s -> s) -> RState s ()
modify f = RState $ \s -> ((), f s)
example :: RState Int String
example = do
x <- get
modify (* 2)
y <- get
return $ "Before: " ++ show x ++ ", After: " ++ show y
main :: IO ()
main = do
let result = runRState example 2333
putStrLn $ show result
It will output
("Before: 4666, After: 2333",4666)
Note that reverse state monad is still in a normal Haskell program. It cannot magically "make time flow backwards". It also cannot magically solve equations to compute old state based on new state. If new state relies on old state it will just deadloop.
Limitations of Haskell lazy evaluation
Haskell lazy evaluation is tied to evaluation order. For a || b, it always try to evaluate a even if b is known to be true. Haskell lazy evaluation cannot be used for solving equations.
Lazy evaluation may also cause memory leak. For example, if you have a large list of integers and you compute sum of it. If the sum value is never used, the list will be still kept in memory for possible evaluation.
Halting problem
Halting problem is proved impossible to solve, by using circular reference.
Assume there exists a function halts(program, input), which takes in a program and input data, and outputs a boolean telling whether program(input) will eventually halt.
Then construct a paradox program paradox:
fn paradox(program: Program) {
if halts(program, program) {
while true {} // dead loop
} else {
return; // halts
}
}
Then halts(paradox, paradox) will cause a paradox. If it returns true, then paradox(paradox) halts, but in paradox's definition it should deadloop.
Rice's theorem is an extension to Halting problem: All non-trivial semantic properties of programs are undecidable (includes whether it eventually halts).
(Note that halting problem cares about whether program halts in finite time, but don't care about how long it takes. A program that need to run 1000 years to complete still halts.)
For a Turing machine, if the states are nodes, then each iteration of running is an edge, jumping from old state to new state. It forms a graph. Not halting is having a cycle in that graph, and that cycle is reachable from beginning state.
Nothing can be analyzed?
Halting problem and Rice's theorem says that we cannot reliably analyze arbitrary Turing-complete programs.
But it doesn't mean nothing can be analyzed. It just means we cannot analyze arbitrary program. There are many analyzable programs. If the program is simple enough, it obviously can be analyzed. If a program use proper encapsulation, analyze can be simplified by only focusing on one part of program.
If we apply some constraints, to make it not Turing complete but still expressive, then halting can be ensured, while being still useful enough, like in Lean.
Rust has a lot of constraints to limit sets of programs to an analyzable subset, so it can analyze about memory safety and thread safety. 1
Non-Turing-Complete programming languages
SQL is not Turing-complete when not using recursive common table extension (with recursive ...) and other procedural extensions (e.g. while).
The proof languages describe both program and proof, according to Curry–Howard correspondence:
- The propositions, like
1 = 1,1 + 1 = 2, correspond to types. If you can obtain a value of that type, you can prove it (what's inside the value is not important for proof, only the type is important). - The function types, like
(x: Integer) -> (x + 0) = xrepresent a propositionx + 0 = x. Pass argument1to that function, you get(1 + 0) = 1 - If you can write a program of that type, without using any side effect , and the program halts, then that theorem corresponding to type is proved.
- A proof can rely on another proof. For example
((x + 1) + 1) + y = 1 + ((x + 1) + y)relies on(x + 1) + y = 1 + (x + y), recursively "call function" until the basic case(0 + 1) + y = 1 + (0 + 1) - To prove theorem corresponding to type
X, "run" a program that returnX. When the program normally finishes and output a value of typeX, it's proved. - If the program don't halt, then value of type
Xcan never be obtained. - That program should not use any side effect (mutation, fail, external IO, randomness, etc.).
- In reality, you just need to ensure the program halts and don't need to really execute the program.
The proof languages, like Lean and Idris, are not Turning-complete. Because a valid proof require the corresponding program to halt. They have special mechanisms (halt checker) to ensure that program eventually halts.
Strictly speaking, Turing complete requires infinitely large memory, so all practical computers and languages don't satisfy strict Turing complete. Apart from memory constraint, blockchain applications often consume fee (gas) in each step of execution, but Turing complete requires unlimited execution steps, so they also not strictly Turing complete.
Ethernet loop
In the raw form of Ethernet, switches don't communicate topology information to each other.
How raw form of Ethernet do routing:
- When it receive a packet from one interface, it knows that the source MAC address correspond to that interface. It's stored into MAC address table. This is self-learning.
- When it doesn't know which interface a MAC address correspond to, it broadcasts packet to all other interfaces, except for the interface that the packet comes from.
It works fine when there is no cycle in network topology. But when there is a cycle, the broadcast will come back to the same switch but from another interface. It not only messes up the self-learning of MAC address table, but can also cause the switch to broadcast the same packet again, and again, causing boradcast storm.
This is solved in spanning tree protocol, where switches share topology information with each other, then break the loop.
Service circular dependency
Sometimes a microservice does some initialization on launch. If that initialization requires using another microservice, then it creates a dependency. If dependency forms cycle, they cannot launch after crashing together.
The best solution is to clearly avoid circular dependency. If that circular dependency initialization is really necessary, make initialization run asynchronously (don't block service starting) and use retrying.
Memory leak even when using GC
In C/C++ if developer forgets freeing then it memory leaks. This is mostly solved by tracing GC.
However it's still possible to leak memory in GC. You can keep adding things into a container and never remove. GC won't collect that because that data is still referenced.
Rice's theorem tells that it's impossible to reliably tell whether program will use a piece of data (unless in trivial case). If an object is unreachable from GC roots, then it obviously won't be used. But if some data won't be used, it may be still referenced. This is the case that tracing GC cannot handle.
Circular reference in math
Circular proof
Circular proof: if A then B, if B then A. Circular proof is wrong. It can prove neither A nor B.
Russel's paradox
The set that indirectly includes itself cause Russel's paradox.
Let R be the set of all sets that are not members of themselves. R contains R deduces R should not contain R, and vice versa. Set theory carefully avoids cirular reference.
Y combinator
Raw lambda calculus only does "string substitution" 2 and doesn't allow a function to directly reference itself. But it can be workarounded by Y combinator:
Written in TypeScript:
type Func<Input, Output> = (input: Input) => Output;
type SelfAcceptingFunc<Input, Output> = (s: SelfAcceptingFunc<Input, Output>) => Func<Input, Output>;
function Y<Input, Output>(
f: (s: Func<Input, Output>) => Func<Input, Output>
): Func<Input, Output> {
// temp = λ x . f (x x)
let temp: SelfAcceptingFunc<Input, Output> =
(x: SelfAcceptingFunc<Input, Output>) => f (input => x(x)(input));
// Note: cannot write f(x(x)), it will deadloop
return temp(temp);
}
const factorial = Y((f: (a: number) => number) => (n) => n > 1 ? n * f(n - 1) : 1);
console.log(factorial(4));
Note that the type of Y combinator requires self-reference, although Y combinator's expression itself don't require self-reference.
Gödel's incomplete theorem
Firstly encode symbols, statements and proofs into data. The statements that contain free variables (e.g. x is a free variable in "x is an even number") can also be encoded (it can represent "functions" and even "higher-order functions").
Specifically, Gödel encodes symbols, statements and proofs into integer, called Gödel number. There exists many ways of encoding symbols/statements/proofs as data, and which exact way is not important. For simplicity, I will treat them all as data, and ignore the conversion between data and symbol/statements/proofs.
is_proof(theory, proof) allows determining whether a proof successfully proves a theory.
Then provable(theory) is defined as whether there exists a proof that satisfies is_proof(theory, proof).
Unprovable is inverse of provable: unprovable(theory) = !provable(theory)
Let H(x) = unprovable(x(x)). Then let G = H(H) = unprovable(H(H)) = unprovable(G) (it uses the same form as Y combinator), which creates a self-referencial statement: G means G is not provable. If G is true, then G is not provable, then G is false, which is a paradox.
The x(x) is symbol substitution. replacing the free variable x with x, while avoid making two different variables same name by renaming when necessary.
Error of error of error...
An error rate can be measured. The measurement, in turn, will have an error rate. The measurement of the error rate will have an error rate ...
We can use the same argument by replacing "measurement" by "estimation" (say estimating the future value of an economic variable, the rainfall in Brazil, or the risk of a nuclear accident).
What is called a regress argument by philosophers can be used to put some scrutiny on quantitative methods or risk and probability. The mere existence of such regress argument will lead to two different regimes, both leading to the necessity to raise the values of small probabilities, and one of them to the necessity to use power law distributions.
- N. N. Taleb, Link
Related
Understanding Real-World Concurrency Bugs in Go
Weakening Cycles So That Turing Can Halt
A Universal Approach to Self-Referential Paradoxes, Incompleteness and Fixed Points
Footnotes
-
Rust can ensure memory safety (when not using unsafe) and is still Turing-complete. This doesn't contradict with Rice's theorem. Because under Rust's constraint memory safety is a "trivial property". ↩
-
Lambda calculus substitutes in a way that avoids naming conflict. It's not simple string substitution. Rigourously speaking, lambda calculus works on abstract lambda terms, not text. Text is just a way of representing them. ↩